La escala numérica utilizada en la regla de cálculo es una tabla de logaritmos. Los logaritmos fueron inventados (o descubiertos, si así queremos decir) por el matemático escocés John Napier de Merchiston en 1619 [4]. La idea es que, dado que 10 al cuadrado es 100, y 10 al cubo es mil, podemos llamar a 2 el logaritmo base 10 de 100 mientras que 3 es el logaritmo base 10 de 1000. En general, si 10 a la potencia 
es igual a 
, es decir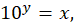 
llamamos a 
el logaritmo base diez de 
. Por ejemplo, con una calculadora podemos verificar que 10 elevado a la potencia 0.5 es 3.16. Por eso 0.5 es el logaritmo base diez de 3.16.
Lo importante de los logaritmos es la regla
,
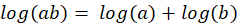la que expresamos diciendo que el logaritmo de un producto de dos números es la suma de sus logaritmos respectivos. Es decir, si tenemos una tabla impresa de logaritmos y queremos multiplicar dos números a y b, miramos en la tabla cuáles son sus logaritmos y los sumamos. Después volvemos a mirar en la tabla para encontrar el número con un logaritmo igual a aquella suma y así obtenemos el producto ab. La multiplicación se convierte de esa manera en adición acompañada de consulta de tablas de logaritmos. Yo aún tuve mis tablas de logaritmos en la secundaria. Las vendían en las papelerías.
La línea de los logaritmos
Podemos considerar a la regla de cálculo, en primer lugar, como una tabla de logaritmos. La escala numérica que contiene es del tipo mostrado en la Fig. 2. El logaritmo de 1 es cero y por eso encabeza la línea. El logaritmo de 2 está representado por la distancia entre el 2 y el 1 en la escala. El logaritmo de tres está representado por la distancia entre el 3 y el 1, y así sucesivamente. Implícitamente tenemos una tabla de logaritmos. Si quiero saber cuál es el logaritmo de 2, solo tengo que medir la distancia entre el 1 y el 2 con una regla. Pero no es necesario hacerlo, la escala numérica de los logaritmos es “autosuficiente” para realizar cálculos.
Por ejemplo, digamos que quiero multiplicar 2 por 2. Abro un compás para capturar la distancia entre el 1 y el 2 (que corresponde a log 2). Con esa apertura y apoyando el brazo izquierdo en el 2, miro hasta dónde llega el otro brazo del compás. Leo en la escala que el resultado es 4 (o sea que log 2 + log 2 = log 4) y con eso obtengo que el producto de 2 x 2 es 4. De la misma manera se pueden multiplicar cualesquiera otros dos números, como el 2 por el 5, para dar como resultado 10 (mostrado en la figura).
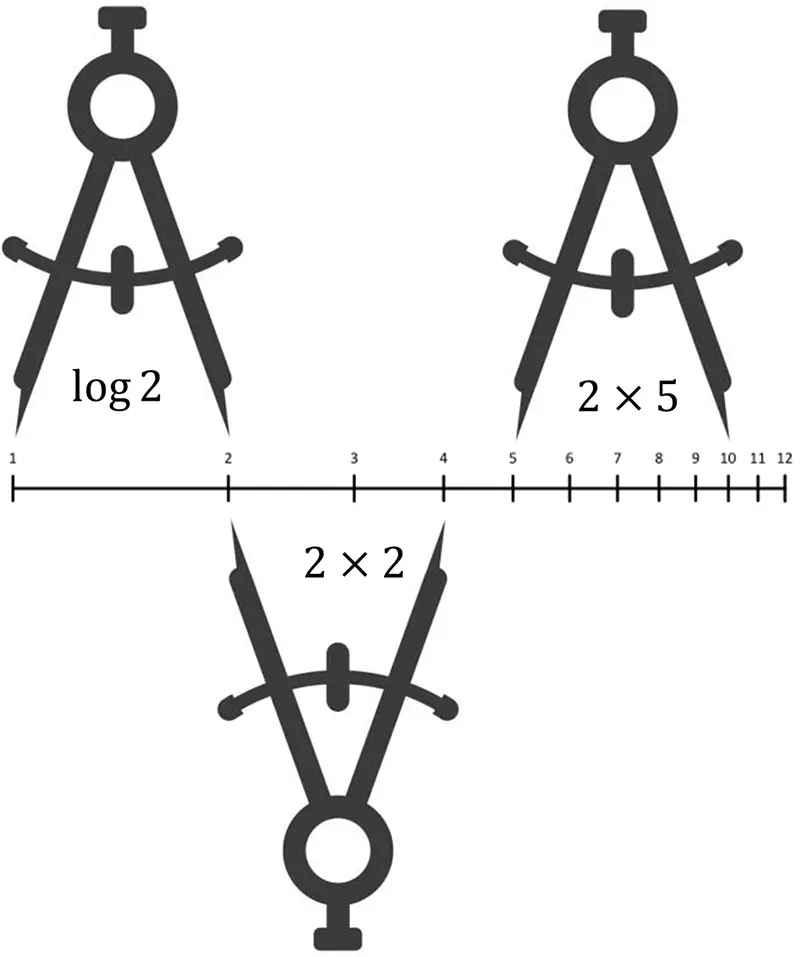
Así es precisamente cómo surgió la regla de cálculo, inicialmente como una línea numérica que encapsulaba una tabla de logaritmos implícita que se podía aprovechar con la ayuda de un compás, con el que puede implementar la adición de distancias.
Esta “línea logarítmica” fue propuesta por Edmundo Gunter, un profesor en Gresham College en Londres, en su libro Canon Triangulorum de 1620 [3]. Por eso la escala fue llamada “Línea de Gunter” y se continuó utilizando durante muchos años (junto con un compás). Es una forma muy ingeniosa de evitar tener que usar tablas de logaritmos, aunque claro que la precisión está limitada por la acuidad visual del usuario y el número de subdivisiones que tengamos en la escala de logaritmos.
La contribución de William Oughtred
El famoso matemático William Oughtred contribuyó tempranamente al desarrollo de la regla de cálculo montando el compás necesario para operar con la línea de Gunter sobre un círculo metálico. La Fig. 4 muestra un ejemplo. La idea de Oughtred fue montar dos brazos móviles en el círculo. La escala logarítmica está ahora dibujada sobre un círculo (con las correspondientes anotaciones numéricas). Los brazos se acomodan entonces para abarcar el logaritmo deseado (log 2, por ejemplo) y luego se mueven acopladas para trasladarlas a cualquier parte de la escala logarítmica, como vimos arriba. Esto a veces es llamado una “regla de cálculo circular”, aunque posteriormente esos instrumentos tendrían partes deslizantes. La idea de Oughtred fue publicada en 1632 por su discípulo William Forster en su libro The Circles of Proportion and the Horizontal Instrument, Londres, 1632 [2].
La regla logarítmica deslizante
En español decimos “regla de cálculo” pero en inglés se dice “slide rule” (o regla deslizante). La idea de estas reglas con partes deslizantes es prescindir por completo del compás o de brazos móviles y ejecutar multiplicaciones o divisiones simplemente desplazando dos escalas contrapuestas. La Fig. 5 muestra la idea.
Como se puede apreciar en la Fig. 5, ahora dos escalas idénticas se desplazan para alinear el 1 de la escala superior con el tres de la escala inferior. El producto 3 por 2 (o sea 6) se encuentra debajo de la marca 2 en la escala superior. Todos los productos de un número por 3 se pueden encontrar abajo de los dígitos respectivos. En esta figura hemos omitido subdivisiones más finas de la escala, pero teniéndolas, es posible multiplicar 3 por 2.5 o 2.7, simplemente mirando el resultado alineado en la escala inferior.
Y aquí es donde arribamos al problema de la prioridad de la invención de la regla de cálculo. Es indiscutible que Edmund Gunter propuso su línea logarítmica en 1620. Se sabe además que Oughtred había mostrado su instrumento a otras personas al menos desde 1630, y posiblemente desde 1627, aunque no existen referencias precisas.
Pero tenemos también al matemático Edmund Wingate, quien escribió un libro con el largo título “The Rule of Proportion in Artithmetick and Geometrie”, publicado primero en Paris en 1624 [5]. Algunos autores afirman que en ese libro se describe la regla de cálculo, en la edición inglesa de 1626. Sin embargo, el historiador Florian Cajori [1] solo pudo detectar la descripción de la regla de cálculo deslizante en otro libro de Wingate con el título “Of Natural and Artificial Arithmetic” de 1630 [6]. Esa descripción se agregó en ediciones posteriores de la “Regla de Proporciones”.
Por eso la conclusión de Cajori es que la prioridad de la publicación de la forma de funcionar de la regla de cálculo deslizante recae sobre Wingate, el popularizador de matemáticas más conocido en Inglaterra en el siglo XVII, aunque la invención ocurrió casi simultáneamente de 1626 a 1630 con Wingate y Oughtred trabajando al mismo tiempo en ideas muy similares. Por eso Cajori concluye: “Edmund Gunter inventó la línea llamada “de Gunter”, pero no la regla de cálculo. La regla de cálculo deslizante fue inventada por Edmund Wingate y fue descrita en varias publicaciones, la primera apareciendo en 1630. Una regla de cálculo similar fue dada al mundo por William Oughtred en 1632, en un trabajo preparado para la imprenta por William Forster. Oughtred fue el primero en diseñar una regla de cálculo circular”.
El sector de proporciones de Galileo
Y finalmente, solo para mostrar que las innovaciones avanzan lentamente y siempre tienen una prehistoria, no podíamos dejar de mencionar el “sector de Galileo”, un instrumento que si bien no inventó el afamado Galileo Galilei (1564-1642), si popularizó durante su tiempo en Padua a finales del siglo XVI. La Fig. 6 muestra una imagen de una regla de proporciones posterior a Galileo, pero que ilustra bien su modo de funcionamiento. Aunque el sector ya existía en formas más simples, Galileo le dio una forma más precisa, versátil y útil para los cálculos matemáticos y prácticos, convirtiéndolo en una herramienta fundamental tanto para científicos como para artilleros e ingenieros.
El instrumento tiene dos escalas numéricas convencionales, representando los números del 0 (en la bisagra) al 10, por ejemplo. El instrumento se abre para formar un triángulo con aquella base dada por la apertura de un compás (que representa X centímetros, por ejemplo). Si colocamos los dos brazos del compás tocando los dos números 7 en ambas escalas, entonces la distancia entre las marcas correspondientes a los números 2, en ambas escalas, corresponde a la apertura del compás X multiplicada por 2/7, por semejanza de triángulos. Si queremos saber cuánto es 3/7 de X, medimos la distancia entre las marcas de los dígitos 3 en ambas escalas, etc. De esta manera contamos con este instrumento con lo que hoy llamaríamos una “computadora analógica” para multiplicar números por fracciones de manera casi instantánea.
Galileo no solo mejoró la precisión del diseño, sino que también escribió un manual, en el que explicaba detalladamente cómo usar el sector para resolver una amplia gama de problemas. Este manual servía como guía tanto para matemáticos como para profesionales militares, y demostraba la utilidad del instrumento en situaciones prácticas.
Conclusiones
Cualquiera que examine una regla de cálculo, rescatada quizás de entre los trebejos de los padres o abuelos, podrá constatar que contiene muchas escalas numéricas, no solo la escala logarítmica tradicional. Lo que sucedió es que, a lo largo de los siglos, se le fueron agregando “tablas” numéricas al instrumento tradicional, como las de las funciones trigonométricas o tablas de cuadrados y cubos, etc. El resultado fue un instrumento muy poderoso para cálculos que no requieren de precisión excesiva, además de ser un compendio de muchas tablas representadas por longitudes para resolver un sinnúmero de problemas numéricos, incluidos los trigonométricos.
En el pasado ya lejano, adquirir la primera regla de cálculo era como un rito de iniciación para estudiantes de ingeniería y ciencias. Aún recuerdo con que orgullo mi padre, un ingeniero, nos llevó a adquirir nuestras reglas de cálculo a mí y a mi hermano gemelo hacia fines de los sesentas. A partir de ahí ya nos habíamos graduado como estudiantes de ciencias, aunque solo cursábamos la escuela secundaria.
Referencias
[1] Florian Cajori, History of the Logarithmic Slide Rule and Allied Instruments, Colorado, 1909.
[2] William Forster, The Circles of Proportion and the Horizontal Instrument, Londres, 1632.John [3] Edmund Gunter, Canon Triangulorum, Londres, 1620.
[4] John Napier, Mirifici Logarithmorum Canonis Descriptio, Londres, 1619.
[5] Edmund Wingate, The Rule of Proportion in Artithmetick and Geometrie, Londres, 1626.
[6] Edmund Wingate, Of Natural and Artificial Arithmetic, Londres, 1630.
