En mi época debíamos acudir a la escuela primaria sin olvidar llevar ciertos instrumentos geométricos, como el compás y la regla. También el “transportador” era imprescindible, aquel semicírculo que sirve para medir ángulos para poder desplazarlos (transportarlos) a otra parte de un dibujo. Sin embargo, existe otro transportador menos conocido y que se utiliza sobre todo en la navegación náutica: se trata del transportador de tres brazos, con el que se pueden fijar dos ángulos al mismo tiempo.
La figura abajo muestra la utilización de dicho transportador. Si tenemos un mapa de la costa y podemos reconocer tres puntos A, B y C sobre ella, y están marcados en nuestro mapa, basta medir el ángulo entre el punto A y B, así como entre B y C, desde la perspectiva del barco, y ajustarlos en el transportador. El navegante puede ahora examinar manualmente desde qué posición en el mapa se pueden obtener los mismos dos ángulos. Es cosa de desplazar el transportador, tocando con los brazos los tres puntos de referencia, hasta acertar con los dos ángulos. El centro del círculo del transportador corresponde a nuestra posición en el mapa.
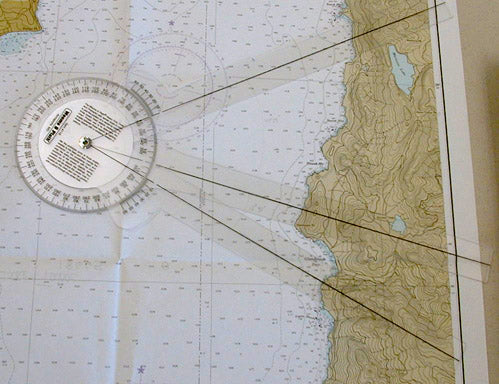
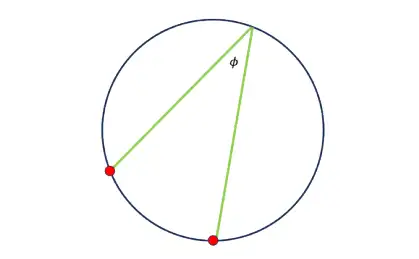
El transportador de tres brazos fue inventado en 1801 por el capitán norteamericano Joseph Huddart, siglos después de que los egipcios construyeron los primeros transportadores simples. No se debe descartar la posibilidad de que el transportador de tres brazos ya fuera conocido antes de Huddart. Pero lo más interesante es: ¿cómo podemos explicar matemáticamente lo que se puede lograr con el transportador de tres brazos? Para explicar esto, pensemos primero que tenemos dos puntos identificados en la costa y que el ángulo entre ellos es Ø, que hemos medido desde nuestra posición (a los matemáticos les gusta usar letras griegas para denotar ángulos). Supongamos que los dos brazos verdes en la figura inferior tienen una apertura igual a ese ángulo. Si desplazamos a los dos brazos, sin variar el ángulo, y siempre en contacto con los puntos rojos, lo que describe el vértice de los dos brazos es un círculo (el arco más corto entre los puntos mismos no está considerado). Dados los dos puntos rojos y el ángulo medido, no sabemos exactamente dónde estamos, pero sí conocemos el círculo de todas las posiciones posibles. Esto lo demostramos más adelante.
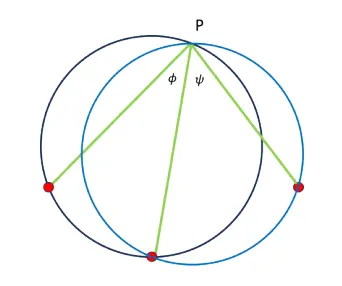
Ahora bien, si tenemos tres puntos conocidos en el mapa y el ángulo entre los dos primeros es Ø, y el ángulo entre el punto intermedio y el tercer punto es Ψ, tenemos ahora dos círculos: el círculo negro trazado por los dos brazos con ángulo Ø y el círculo azul trazado por los dos brazos con el ángulo Ψ. Los dos círculos se interceptan en nuestra posición P. La solución la leemos directamente en el mapa.
No es difícil demostrar que, si trazamos con el transportador la curva de nuestra posición, manteniendo la apertura de dos brazos fija, lo que obtenemos es un círculo. La figura abajo muestra la idea. Tenemos dos puntos de referencia (marcados con rojo). Si mantenemos fijo el ángulo θ formado por dos líneas que pasan por los dos puntos rojos, el punto de cruce de las dos líneas describe un círculo al desplazar al ángulo de derecha a izquierda (moviéndonos de los trazos azules, a los verdes y a los amarillos).
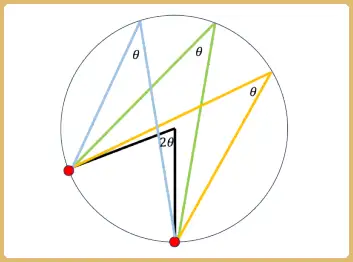
Para hacer esto plausible, demostramos que, si tomamos un círculo con dos puntos de referencia (en rojo, abajo), el ángulo formado por las dos rectas verdes es igual a la mitad del ángulo formado por las rectas azules, mismas que pasan por los puntos de referencia y el centro del círculo. Ya que el ángulo formado por las líneas azules es constante, lo mismo sucede con el ángulo formado por las líneas verdes, sin importar dónde se encuentre su punto de cruce sobre el círculo (véase la figura anterior).
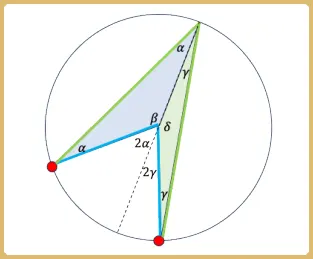
Ilustremos todo eso con un caso especial, pero suficientemente ilustrativo. En la figura arriba tenemos dos triángulos (uno azul y el otro verde). Ya que la suma de sus ángulos debe ser 180 grados, tenemos que:
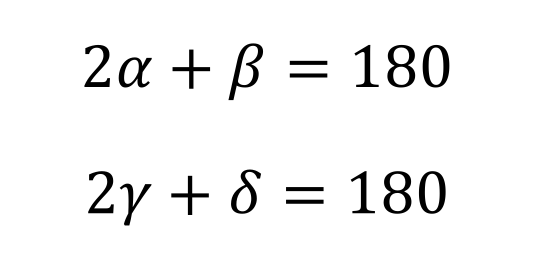
Eso implica que el ángulo complementario a β es 2α, mientras que el ángulo complementario a δ es 2γ. Ahora bien, el ángulo entre las líneas azules es 2α + 2γ, que es el doble del ángulo α + γ, entre las líneas verdes, como queríamos demostrar. Ya que 2α + 2γ es constante, lo mismo sucede con α+ γ
Con esto queda claro por qué el transportador de tres brazos puede ser usado exitosamente para triangular la posición de un barco en un mapa utilizando tres puntos de referencia.
Quizás es interesante añadir que vehículos autónomos se orientan en el tráfico utilizando puntos de referencia, anotados en un mapa, que son detectados con la ayuda de unidades láser (Lidar). Dado el gran margen de error que tienen esas mediciones en movimiento, se utilizan cientos o miles de puntos de referencia en lugar de los tres aquí mencionados. Es como llevar en el auto un transportador electrónico con miles de brazos computarizados.






