El Teorema de Viviani

Hay un teorema sobre triángulos equiláteros que suena contraintuitivo cuando se topa uno con él por primera vez, pero que es fácil de demostrar. Supongamos que tenemos una isla que tiene la forma de un triángulo con tres lados iguales (un triángulo equilátero).

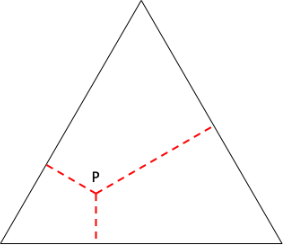
Si quisiéramos acampar en un punto de la isla de manera que la suma de las distancias a los tres lados sea mínima, ¿Cuál sería la mejor posición para instalar la tienda de campaña? La distancia hacia los tres lados se mide perpendicularmente a ellos, desde el campamento. La figura muestra una isla como la propuesta, con tres lados iguales y un posible punto P para acampar. Las líneas rojas muestran las distancias hacia cada lado.

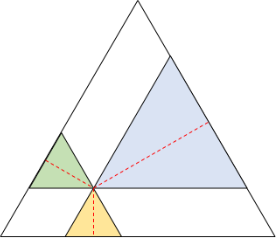
Podemos imaginar que, apoyándonos en el punto P, dibujamos tres triángulos semejantes al triángulo original (mostrados abajo, coloreados). La distancia hacia los lados representa la altura de cada triángulo. Eso es lo que queremos sumar.

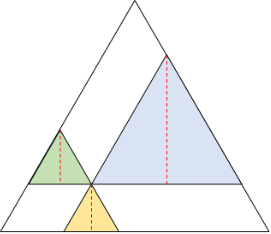
La altura de cada triángulo de color es la misma, desde cualquier vértice que la midamos (porque son triángulos equiláteros). La figura que sigue nos muestra las alturas de cada triángulo de color, ahora medidas verticalmente. La suma sigue siendo la misma.

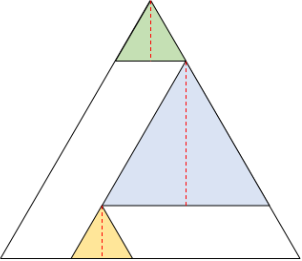
Finalmente, deslizamos el triángulo verde hasta el vértice superior del triángulo original, lo cual es posible, como se desprende de la construcción geométrica. Es fácil ver ahora que la suma de las alturas de los tres triángulos de color corresponde a la altura del triángulo original. Ya que esto es válido para cualquier punto P en la isla, eso significa que la suma de las distancias hacia los tres lados es siempre la misma, independientemente de la ubicación del punto P. Es decir, es irrelevante dónde coloquemos la tienda de campaña; la suma de las distancias a las tres playas de la isla se mantiene constante y es igual a la altura del triángulo representado por la isla.

 
Este es el llamado "Teorema de Viviani", que lleva ese nombre en honor a Vincenzo Viviani (1622-1703), un discípulo del renombrado Galileo Galilei, con el que comenzó a colaborar en 1639. El teorema que lleva su nombre fue una sola de las muchas contribuciones de Viviani en el terreno de las matemáticas y la física. Además, el teorema se puede generalizar para polígonos regulares con más de tres lados.