A los matemáticos les gusta investigar formas, superficies y volúmenes que tienen propiedades contraintuitivas. Es el caso de la “esponja de Menger”, así llamada en honor del matemático austriaco Karl Menger (1902-1985), quien hace exactamente cien años la describió. Es aquella precisamente la época en la que se proponen muy diversas funciones “monstruo”, destinadas a mostrarnos cómo la intuición de la vida diaria nos puede fallar cuando analizamos objetos matemáticos de manera rigurosa.
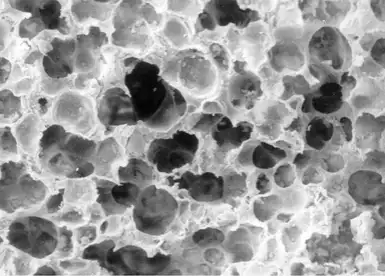
La figura de abajo muestra a la esponja, la cual consiste en un cubo con muchos orificios colocados estratégicamente. Para generar la esponja partimos de un cubo que subdividimos en 27 minicubos, cada uno con lados que tienen un tercio de la longitud de los lados del cubo original (imaginemos un cubo de Rubik). En el primer paso eliminamos los minicubos centrales en cada una de las seis caras del cubo original, así como el minicubo en el centro del cubo. En total eliminamos así siete minicubos. En el segundo paso tomamos cada minicubo, lo transformamos en 27 miniminicubos y repetimos la misma operación de remoción de material con cada uno de ellos. Si continuamos recursivamente de esta manera, obtenemos algo parecido a la figura de abajo, que no representa el límite del proceso, sino un estado intermedio después de cuatro iteraciones. En el límite, el cubo original queda horadado por todos lados y la primera pregunta que habría que hacer es cuánto volumen contiene al final y cuál es la superficie de sus caras.

Sorprendentemente, la esponja de Menger tiene volumen cero, ¡pero superficie infinita! Lo podemos calcular de manera sencilla.
Si el cubo tiene lados de longitud 1, el volumen inicial es 1. Al remover 7 minicubos con cantos de longitud 1/3, nos quedan 20 minicubos con cantos de longitud 1/3. El volumen inicial es V0 =20/27. El volumen restante, después de la primera iteración, es V1 =20/27. Si ahora a cada minicubo se le eliminan 7 miniminicubos con cantos de largo (⅓)², nos quedamos con 20² miniminicubos de los 27² originales. El volumen de la construcción es ahora V2 = (20/27)² . Y así sucesivamente en cada iteración. Después de tres pasos el volumen disminuye a V3 = (20/27)³, y después de diez pasos ya solo nos queda un volumen de V10 = (20/27)¹⁰ (cinco por ciento del volumen original). Es decir, el volumen de la esponja de Menger converge a cero en un número infinito de pasos.
¿Qué sucede con la superficie de la esponja? Al principio la superficie es igual a 6, por las seis caras del cubo original. Ahora hay que proceder con cuidado: al recortar seis minicubos de las seis caras, tenemos 6(⅓)² menos área. Pero los seis orificios creados tienen cada uno un área adicional de 4(⅓)², lo que en total sería un área adicional de 24(⅓)². Ya que el minicubo central no genera nueva área, nos queda finalmente un área adicional de
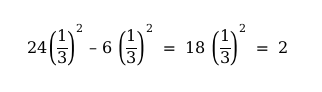
Es decir, en el primer paso del algoritmo para generar la esponja de Menger, la superficie total pasa de 6 a 8, un aumento del 33 %. En los pasos subsecuentes tenemos que ser más cuidadosos al contar, porque cada minicubo no expone sus seis lados al “aire”. Hay caras de los minicubos que están en contacto entre sí y que no debemos agregar al cálculo del área total. Se puede demostrar, sin embargo, que en n iteraciones del algoritmo la superficie de la esponja provisional así generada tiene una superficie igual a
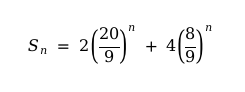
Es fácil ver que esta expresión aumenta sin límite al aumentar el número de iteraciones n. En el límite final, la superficie de la esponja de Menger es infinita.
Es curioso que un objeto que no tiene volumen pueda tener una superficie infinita, pero así es en la geometría. Por ejemplo, un plano ilimitado no tiene grosor, por lo que su volumen es cero, pero su superficie es infinita.
En el mundo de la física existen materiales que, sin llegar a ser una esponja de Menger, sí nos remiten a esa relación contraintuitiva entre volumen y superficie. Un material así es la zeolita, un mineral cristalino poroso que tiene muchas aplicaciones. La zeolita tiene tantos poros que un gramo de zeolita contiene una superficie de 300 metros cuadrados. En un kilogramo de zeolita encontramos una superficie expuesta de ¡300 mil metros cuadrados! Por eso se ha pensado en la zeolita para catalizar procesos químicos que dependen de la química de superficies. En la construcción de baterías para aparatos eléctricos también se ha buscado utilizar materiales con una relación área/volumen lo más alta posible. El carbono poroso ha sido una buena alternativa.

Los humanos transportamos en nuestro cuerpo un órgano poroso que no tiene nada que envidiarle a la esponja de Menger. Se trata de los pulmones, cuyos alvéolos se ramifican de manera que maximizan la superficie expuesta al intercambio de oxígeno y CO2, mientras que minimizan el peso total del órgano. Aunque no existe un consenso médico, muchas veces se dice que la superficie de los pulmones puede cubrir un área de unos 70 metros cuadrados, mientras que el peso promedio de ambos pulmones, en adultos, va de 1.0 a 1.3 kilogramos. Los alvéolos logran esta gran área doblándose y redoblándose, como origamis orgánicos, para posibilitarnos absorber todo el oxígeno posible del aire. Podemos pensar en los pulmones como nuestra fuente de energía, que no aparece plana, como las grandes celdas solares de los satélites de telecomunicaciones, sino que están tan bien doblados que los podemos alojar en nuestro pecho.