Muchos habrán escuchado la célebre frase atribuida al matemático griego Arquímedes: “Dadme un punto de apoyo y moveré al mundo”. Este dictum se refiere a las leyes de la palanca. Mientras más largo es el brazo de una palanca, mayor es el peso que se puede levantar en el otro extremo, de brazo corto. Sin embargo, no todos saben que Arquímedes analizó exhaustivamente las llamadas “leyes de las palancas” en un famoso texto que lleva por título “Sobre el equilibrio de los planos”, que probablemente escribió en Siracusa entre 270 y 250 años antes de nuestra era.
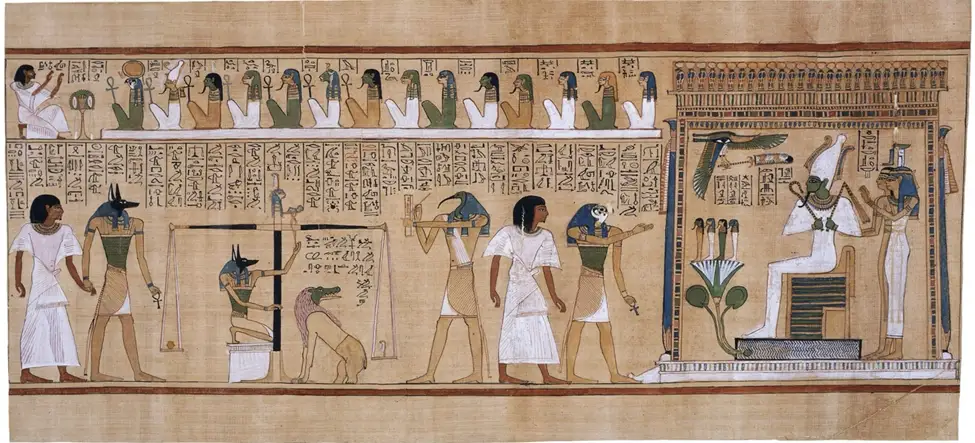
En la historia previa a Arquímedes ya había antecedentes. Las balanzas fueron utilizadas por los egipcios y babilonios para comparar el peso de objetos con el de pesas normadas. Existen restos arqueológicos y pinturas egipcias mostrando los dos platos de una balanza y la forma en que eran construidas. La balanza tiene normalmente dos brazos rígidos que pueden girar alrededor de un fulcro o punto de apoyo. Los platos de la balanza se pueden colocar sobre el brazo rígido o colgando de él. Era tan conocida la balanza para los egipcios, que creían que las almas eran pesadas por las deidades después de la muerte utilizando precisamente una balanza (véase la figura adjunta).
Los axiomas de Arquímedes
Lo peculiar del método de Arquímedes para analizar las balanzas es que resuelve un problema de mecánica utilizando argumentos geométricos, basados en simetrías. Procede de manera axiomática, estableciendo verdades “incontrovertibles”, de las que se desprenden conclusiones ya no tan evidentes.
Las leyes de la balanza propuestas por Arquímedes son las siguientes:
1) Si se colocan pesos iguales en ambos lados de la balanza, a la misma distancia del fulcro, la balanza está en equilibrio.
2) Si tenemos pesos en equilibrio y agregamos peso en un lado de la balanza, ésta se inclina hacia ese lado.
3) Si tenemos pesos en equilibrio y tomamos peso de un lado de la balanza, ésta se inclina hacia el lado contrario.
Nada de esto es sorprendente. En el caso (1), si los pesos son iguales y están colocados a la misma distancia del fulcro, por simetría geométrica no podemos pensar que la balanza se pueda inclinar hacia alguno de los dos lados. Los casos (2) y (3) corresponden a la experiencia.
Además de estos sencillos axiomas, Arquímedes opera con el concepto de “centro de masa”. Este es el punto sobre el que se puede apoyar un objeto sin que este se incline hacia un lado o hacia el otro. La figura adjunta muestra una balanza doble. Los platos de la balanza son a la vez sendas balanzas (con fulcros A y B, respectivamente). Por simetría de la construcción, ninguna de las dos balanzas superiores, y tampoco la inferior, se puede inclinar ni hacia la izquierda ni hacia la derecha de los fulcros A, B y C.

Supongamos ahora que colocamos los dos pesos de la balanza de la izquierda el uno sobre el otro. Tenemos otra configuración mecánica, pero, por simetría, las balanzas continúan en equilibrio.
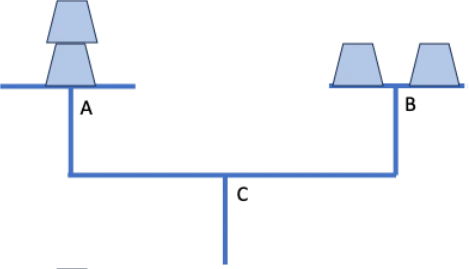
Lo que esto quiere decir es que en un problema mecánico podemos considerar que todo el peso de un objeto se ejerce sobre el centro de masa. Los dos pesos de la izquierda, considerados como un solo objeto, tienen un centro de masa colocado precisamente sobre el fulcro A. El peso de los dos objetos se ejerce sobre ese fulcro A y balancea los otros pesos en el plato de la derecha.
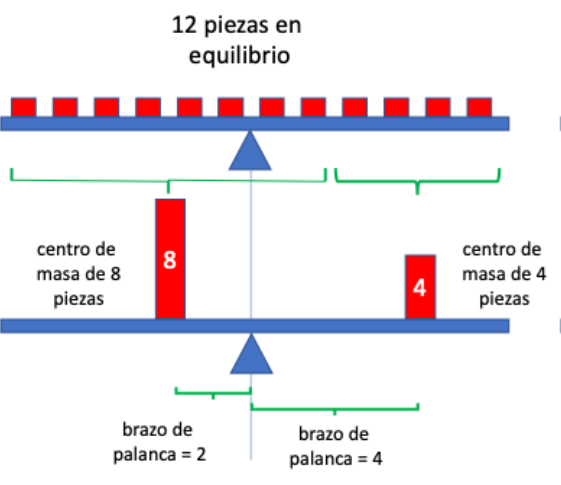
Una ingeniosa construcción geométrica le permite a Arquímedes demostrar la ley general de la palanca, que dice simplemente que, si colocamos dos masas M y N a las distancias m y n, respectivamente, del fulcro, entonces los productos Mm y Nn son iguales, i.e., Mm=Nn. La figura inferior muestra la argumentación de Arquímedes.
Comenzamos con 12 piezas rectangulares en equilibrio sobre el fulcro de una balanza. Ahora bien, podemos agrupar ocho piezas, comenzando desde la izquierda, y las sustituimos por un peso equivalente situado en su centro de masa (la barra roja marcada con 8). Lo mismo hacemos con las cuatro piezas restantes (barra roja marcada con 4). El lector puede verificar que los brazos de palanca son, respectivamente, 2 y 4. La balanza sigue en equilibrio porque 8x2 =4x4 Esta es la ley general de la palanca.
El lector puede verificar que hay otras particiones posibles de las 12 piezas, pero todas satisfacen la ley de la palanca. Por ejemplo, 6 y 6 piezas, en cuyo caso 6 x 3= 6 x 3. O bien 10 y 2 piezas, en cuyo caso 10 x 1 =5 x 2
El producto del peso de un objeto, multiplicado por la distancia a un punto de giro, es importante en la física. Se le llama “torque” y por eso podemos simplemente decir que una balanza está en equilibrio cuando el torque positivo en un plato de la balanza contrarresta el torque negativo del otro plato. En una balanza en equilibrio, el torque total es cero.









