Hay muchos ejemplos de figuras fractales, es decir, figuras geométricas que tienen una cierta forma, la que reaparece en miniatura al inspeccionarlas más de cerca. El llamado triángulo de Sierpiński es un buen ejemplo. El triángulo se repite en su interior tres veces, y en cada uno de esos tres triángulos interiores aparece de nuevo tres veces, y así hasta el infinito.

Hay un rectángulo de proporción famosa entre sus lados ortogonales, la llamada “razón dorada”, que ha sido tematizada desde la antigüedad clásica. Un rectángulo en proporción dorada es aquel con dos lados ortogonales en proporción
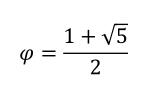
que es aproximadamente φ=1.618. Supuestamente, la razón dorada sería especialmente estética y por eso habría sido utilizada en la arquitectura helénica. No vamos a discutir eso, pero sí vamos a mostrar que un rectángulo en razón dorada es una especie de fractal, ya que el rectángulo original reaparece en miniatura cuando lo reducimos de la manera que vamos a detallar.
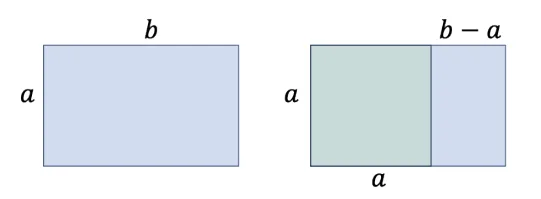
Dado un rectángulo en razón dorada, con lados y , lo podemos dibujar (abajo a la izquierda). Si recortamos el máximo cuadrado que podemos alojar en su interior, obtenemos la figura de la derecha. El pequeño rectángulo azul es una versión en miniatura del rectángulo original.
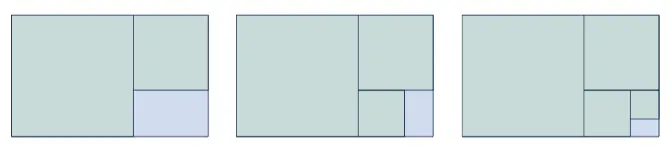
Podemos continuar con este proceso de recortar cada vez el cuadrado mayor posible del rectángulo azul, y el rectángulo reaparece con las mismas proporciones una y otra vez. Esto es lo que define a un rectángulo con lados en razón dorada. Se trata de un rectángulo fractal bajo la operación geométrica que estamos considerando.
Podemos encontrar el valor numérico de la razón dorada asignándole el valor 1 al lado de longitud (ya que lo que importa es solo su proporción con b). Si las proporciones del rectángulo de lados (), son las mismas que las del rectángulo con lados (a, b-a), entonces:
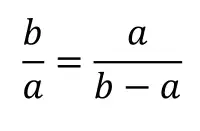
Con a=1, tenemos
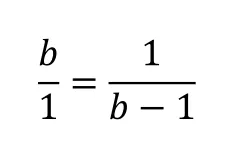
O sea que b² -b =1 La solución de esta ecuación cuadrática es precisamente φ=1+√5/2, como el lector puede comprobar.
Yo pienso que la fascinación con φ, la razón dorada, proviene de nuestro interés intrínseco por todas las figuras fractales y sus simetrías.
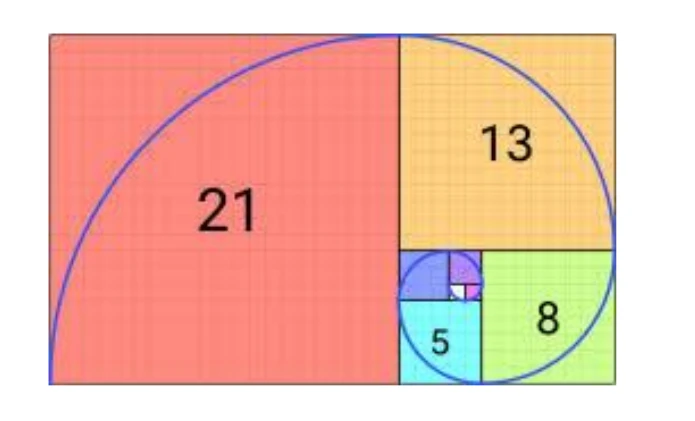
Curiosamente, si construimos rectángulos con lados ortogonales iguales a dos números de Fibonacci consecutivos, obtenemos la razón dorada. La sucesión de Fibonacci comienza con los dos números 1, 1, y continúa con la suma de los dos últimos números de la sucesión, o sea así: 1, 1, 2, 3, 5, 8, 13, 21, 34, etc. La fórmula general es
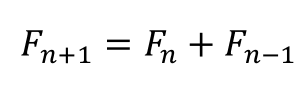
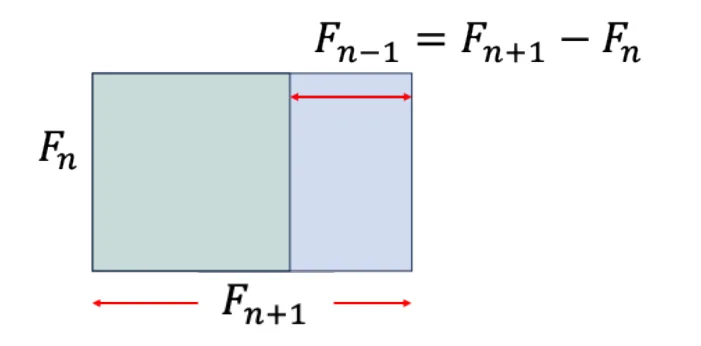
El rectángulo dibujado abajo tiene lados a=Fₙ, b=Fₙ₊₁ , y como se puede ver la diferencia de los dos lados es b-a=Fₙ₋₁, exactamente como en la construcción del rectángulo con razón dorada con el que comenzamos esta exposición.
En la figura de colores abajo encontramos números de Fibonacci sucesivos. El rectángulo original tiene lados de longitud 34 y 21. Al ir extrayendo cuadrados máximos, vamos reproduciendo los números de Fibonacci, en el largo de los lados de cada cuadrado sucesivo.
En cada cuadro de color se ha dibujado además un cuarto de un círculo; el resultado es una curva conexa y en espiral que ha sido llamada “la espiral dorada”. Se ha tratado de encontrarla reproducida en la naturaleza (por ejemplo, en la concha de los nautilos), pero se trata simplemente de una curiosidad matemática. La concha de los nautilos corresponde en realidad a una espiral logarítmica.