Siguiendo el ejemplo de Richard Dedekind, quien se preguntó para qué sirven los números, podemos plantear una pregunta similar, pero ahora respecto a la unidad de medida de ángulos llamada radián.
Si pensamos en un círculo y una manecilla anclada en su centro y girando, podríamos medir su avance utilizando las marcas en la carátula de un reloj. Sin embargo, ya desde la época de los babilonios y la antigüedad clásica se utiliza una partición del círculo en 360 partes iguales. Es lo que llamamos una subdivisión en “grados”. En la escuela primaria utilizamos un semicírculo dividido en 180 grados, que nos sirve para medir los ángulos de figuras geométricas.
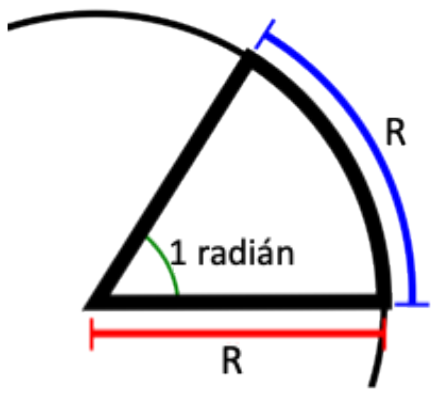
Existe, sin embargo, otra unidad de medida para los ángulos, que es más natural: es el llamado radián. El ángulo formado por dos radios en un círculo es un radián, si el arco que limitan sobre su periferia es de la misma longitud que el radio. Mientras que la subdivisión del círculo en 360 grados es arbitraria (podrían haber sido 720 subdivisiones, o solo 90), la subdivisión utilizando el radio del círculo es más natural.
Expliquémoslo de otra forma: si llegáramos a tener contacto con una civilización extraterrestre, para ellos el círculo podría estar dividido en 500 partes iguales. No hay justificación alguna para el tamaño que quisieran asignar a sus “grados”, así como la partición del círculo en 360 grados, solo se justifica porque podemos dividir fácilmente al círculo en mitades, tercios, cuartos, sextos, octavos y hasta doceavos. Todas esas piezas tienen un número entero de grados.
De hecho, ha habido otras propuestas. Durante la Revolución Francesa se formalizó la división del círculo en 400 partes iguales. Cada parte se llama un “gon” o “gradian”, y este tipo de subdivisión, aunque no se popularizó más allá de las mediciones geodésicas y la minería, aún se utiliza en partes de Europa. Cada gon se puede dividir en decigones, centigones y miligones, al aplicar el sistema decimal al círculo.
Como decíamos, una unidad de medida más natural, nno sujeta a la historia ni a sus peripecias, es el radián, dado que el perímetro P de un círculo es directamente proporcional al radio R del mismo (ya que P= πR). Por eso, lo más natural es tomar el ángulo abarcado por un arco del círculo igual al radio del mismo. Esta definición es natural y universal, fácil de entender para cualquier cultura, incluso extragaláctica. un radián equivale a 57,3 grados, aproximadamente. Esto es porque un círculo abarca 2π radianes (recordemos otra vez que P= πR), que equivalen a 360 grados. Por eso un rad, como se abrevia, es igual a 360/2π grados.
El primer matemático que dejó constancia impresa de la utilización de la nueva unidad fue el inglés Roger Cotes (1682-1716), quien lo utilizó en su obra “Logometría” de 1714, dedicada a Edmund Halley. No la llamó “radián”, esto fue hecho posteriormente por los matemáticos James Thomson (que utilizó el concepto desde 1871) y por Thomas Muir en la Universidad de San Andrés en Escocia, que lo utilizó en sus exámenes entre 1869 y 1874. Cuando Thomson y Muir discutieron asignarle un nombre definitivo a la nueva unidad, decidieron usar “radial”, como abreviatura de “radial angle”, que posteriormente se convirtió en “radián”.

Pero como siempre que de las matemáticas británicas y continentales se trata, encontramos orígenes múltiples para los conceptos. Resulta que el gran Leonhard Euler también utilizó al radián, de manera implícita, en su obra “Introductio in analysin infinitorum” de 1748, con lo que simplificó fórmulas trigonométricas y expansiones en series de las mismas. De hecho, fue Euler quien popularizó el uso de lo que él llamaba “medida circular”. El matemático alemán Georg Simon Klügel incluyó la “medida circular” en su libro de texto “Trigonometría Analítica” de 1770.
Los griegos adoptaron a la larga el sistema babilónico de 360 grados para un círculo, pero Euclides (alrededor de 300 a. C.) no trabajaba con el concepto de “grados”. La unidad de comparación eran los ángulos rectos, formados por líneas ortogonales. Ángulos eran menores o mayores que un ángulo recto, o abarcaban una fracción del mismo. Alrededor de 200 a. C., el astrónomo Hiparco adoptó los 360 grados de los babilonios y la tradición se extendió hasta El Almagesto de Ptolomeo, la obra cumbre de la astronomía de la antigüedad. Y es por eso que aún hablamos de los 360 grados de un círculo, pero para calcular algo utilizamos radianes.
Es el peso de la historia concentrado en el círculo.





