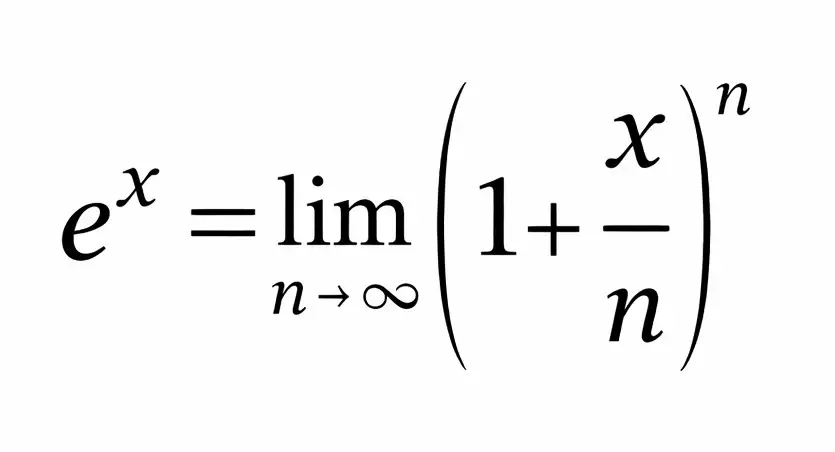El número e

En las matemáticas existen algunas constantes muy importantes, por sus aplicaciones en diversas áreas. En la geometría, el número π es central: equivale a la relación entre el perímetro de un círculo y su diámetro. Esta proporción es universal, es la misma para cualquier círculo.

Otro número que aparece de manera natural cuando consideramos procesos de crecimiento es el número e, que fue bautizado así por el matemático suizo Leonhard Euler (1707-1783) y que por eso es conocido como la “constante de Euler”. Su valor aproximado, a cinco decimales, es 2.71828. Esta constante es un número de los llamados irracionales porque no se pueden escribir más que con una cantidad infinita de cifras después del punto decimal.

El número 𝑒 aparece de manera natural en un ejemplo, propuesto por Jacob Bernoulli (1655-1705), relacionado con el interés compuesto y que sirve como modelo matemático de procesos de crecimiento. Para entender cómo aparece e, tenemos que considerar cómo funciona el interés compuesto.

Si tenemos un peso y lo invertimos al 100% de interés anual, con pago al final del período, recibimos 2 pesos después de un año. Sin embargo, si los pagos son semestrales, el peso inicial se convierte en 1.5 pesos a los seis meses (el peso inicial más 50% de interés). Pasados otros seis meses, si el dinero sigue invertido, recibimos 1.5 pesos más 50% de interés sobre 1.5 pesos, que son 0.75 pesos. El pago final es de 2.25 pesos.

En el primer caso, con capitalización anual, el dinero crece de 1 a 2 pesos. Decimos que el factor de crecimiento es 2. En el segundo, con capitalización cada seis meses, el peso invertido se transforma en 2.25 pesos y el factor de crecimiento es 2.25.

Como podemos observar, al inversionista le conviene que el interés se capitalice cada seis meses y no cada doce, aunque la tasa de interés nominal anual siga siendo de 100%. Con capitalización cada seis meses, la tasa de interés real es de 125% sobre el peso inicialmente invertido. Es decir, el factor de crecimiento de la inversión es mayor mientras más frecuentemente se capitalicen los intereses.

Podemos ahora generalizar. Si el inversionista logra capitalizar el interés cada tres meses, la tasa nominal cada tres meses es de 25% (o sea, 100% dividido entre cuatro períodos). El dinero crece en esos cuatro períodos: primero de 1 a (1+0.25), luego a (1+0.25)², en el tercer trimestre a (1+0.25)³, y en el cuarto hasta (1+0.25)⁴. Como vemos, la fórmula general del factor de crecimiento, para n períodos de capitalización, es:

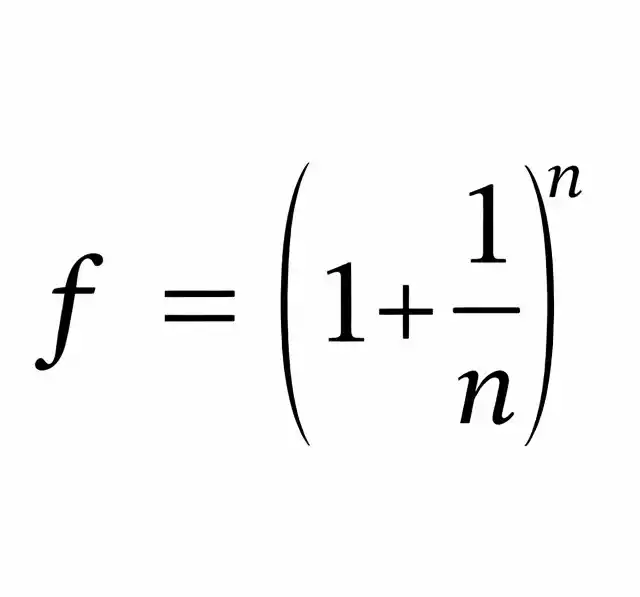
Partiendo de una tasa nominal de 100% de interés, el interés por período es 1/n. La tabla que sigue muestra cómo varían el interés por período, cuándo varía y cómo varía el factor de crecimiento. Lo interesante de la tabla es que el factor de crecimiento no explota hacia infinito al ir capitalizando el dinero en intervalos cada vez más cortos. El factor se va aproximando a un límite, que es precisamente la constante de Euler. Ya para n=100 el factor de crecimiento es de 2.705, muy cercano a la aproximación mencionada arriba de 2.71828.

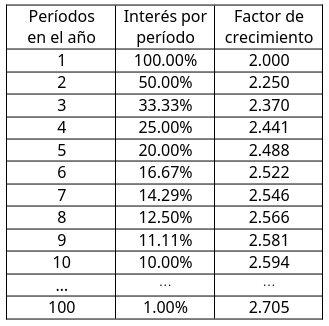
En otras palabras, el valor numérico de la constante de Euler corresponde al factor de crecimiento de una inversión de un peso, a interés nominal de 100%, cuando el interés se capitaliza instantáneamente.

No lo vamos a demostrar, pero basta agregar que, si la tasa de interés anual no es 100%, sino que tiene valor x, el factor de crecimiento de una inversión de un peso capitalizada instantáneamente (cuando el número de intervalos en el año crece a infinito) es: