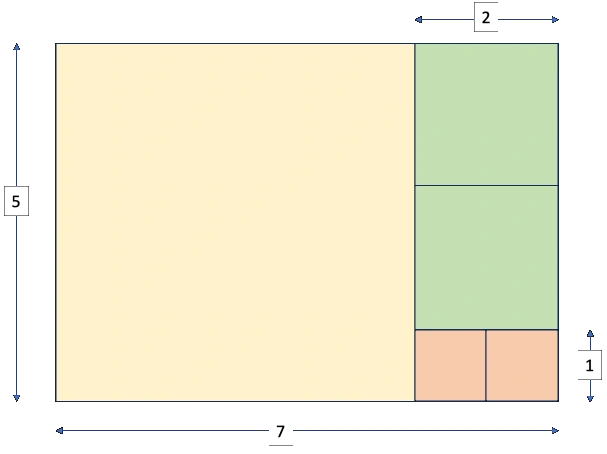
A veces un número entero puede ser dividido de manera exacta por otro entero, por ejemplo, 15 es divisible por 3. En este caso decimos que 3 es un “factor” de 15. Un número puede tener diversos factores. Por ejemplo, 15 es divisible por los números 1, 3, 5, y 15.
Dados dos enteros, nos podemos preguntar cuales factores poseen en común y cuáles el mayor de ellos. Por ejemplo, el 6 y el 12 tienen cuatro factores comunes, que son 1, 2, 3, y 6. Al factor común más grande lo llamamos el “máximo común divisor” (MCD). En este caso el MCD de 6 y 12es 6. Si tomamos el 6 y el 15, suMCDes 3.Hay números, como el 5 y el 7, que solo tienen al 1 como divisor común. En este caso su MCD es 1.
A muchos nos enseñaron en la escuela primaria a encontrar el MCD de dos números. Una manera de hacerlo es recurrir a los llamados números primos (aquellos que no son divisibles por un entero menor, distinto de 1). Por ejemplo, podemos escribir 6=2×3 y también 15=3×5. Vemos de inmediato que solo poseen un factor común mayor que 1, es decir, el número 3. Éste es el MCD de 6 y 15.
Para números más grandes esta estrategia de factorizar a ambos para comparar los factores comunes no es muy eficiente. Por eso para encontrar el MCD de dos números desde la antigüedad se utiliza el “Algoritmo de Euclides”. El método es llamado así en honor al célebre matemático griego de Alejandría.El algoritmo de Euclides procede por divisiones sucesivas, como en el ejemplo mostrado abajo:
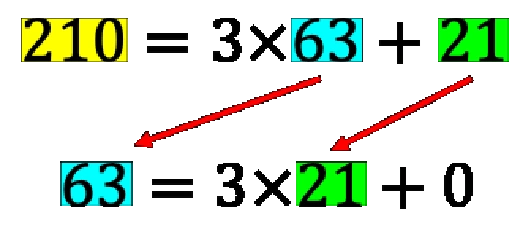
Lo que muestra este ejemplo es que 21 divide exactamente a 63 (63 dividido por 21 es 3) y además como 210 contiene tres veces al 63 y una vez al 21, el 21 divide exactamente a 210 y a 63. Es un factor común y además, como se puede demostrar, es el máximo factor común posible.
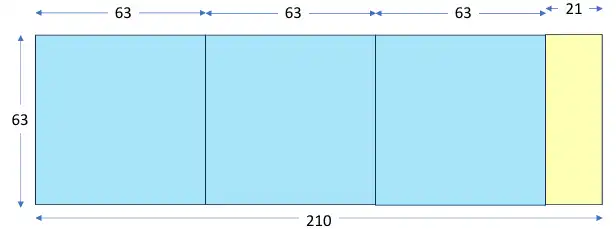
Hay una manera de visualizar al algoritmo de Euclides de divisiones sucesivas utilizando una figura geométrica. Supongamos que queremos encontrar el MCD de los números 210 y 63. Dibujamos entonces un rectángulo con un lado de 210 unidades y el lado adjunto de 63, como muestra el diagrama.

En el algoritmo de Euclides se calcula cuantas veces cabe el número más pequeño (en este caso 63) en el número más grande (210). La respuesta es tres. Se puede visualizar este hecho pensando que llenamos el rectángulo original con los cuadrados más grandes que podemos dibujar en su interior. En este caso podemos alojar tres rectángulos de 63 unidades por lado en el rectángulo amarillo. El resto no cubierto es un rectángulo, con su lado menor de longitud 21.
Ahora lo que queremos hacer es recubrir al rectángulo restante, en amarillo, con los cuadrados más grandes posibles. Es fácil ver que tres cuadrados de 21 unidades por lado (en verde) cubren el resto del rectángulo amarillo.
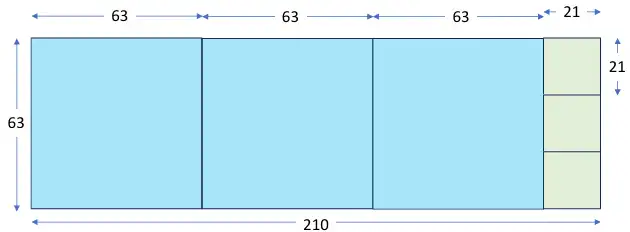
El algoritmo termina cuando ya todo el rectángulo original ha sido cubierto con cuadrados de diversos tamaños. La longitud de cada lado del cuadrado más pequeños es igual al MCD de los números originales.
En el ejemplo anterior encontramos que 21 es el MCD de 210 y 63. El diagrama nos lo muestra: 21 cabe tres veces en 63 (véanse los cuadrados azules). Si el 21 cabe tres veces en 63, el diagrama anterior nos muestra también que 210=3(3×21)+21=10×21=210.
No hay otro factor común que sea mayor que 21. Si lo hubiera, el algoritmo hubiera terminado con cuadrados con longitud por lado mayor a 21.
El ejemplo final que queremos mostrar es el de los dos números 5 y 7, que no tienen otro factor común mayor a1. El diagrama muestra el desarrollo del algoritmo de Euclides, que termina con cuadrados de lado igual a 1. Hemos omitido especificaciones redundantes de las longitudes de los ladosde los cuadrados.