Si pensamos en objetos presentes en nuestro mundo tridimensional podríamos preguntar si existe una superficie que tenga solamente un lado (es decir, no la podemos colorear por adelante y por atrás con dos colores distintos) y que esté limitada por un solo margen. Acostumbrados como estamos a pensar en términos de superficies de papel o plástico moldeado, pareciera que una cosa sí no existe. Un poco más de reflexión nos conduce a un objeto que los niños pueden usar para divertirse: la llamada banda de Möbius, en honor del matemático August Ferdinand Möbius, quien la describió en 1858.
Para confeccionar la banda, basta con tomar una cinta de papel y pegar sus dos extremos, pero girando uno de los lados para que no se forme una especie de cinturón. El diagrama inferior muestra el resultado, después de adherir sus dos extremos (rotando primero uno de ellos).
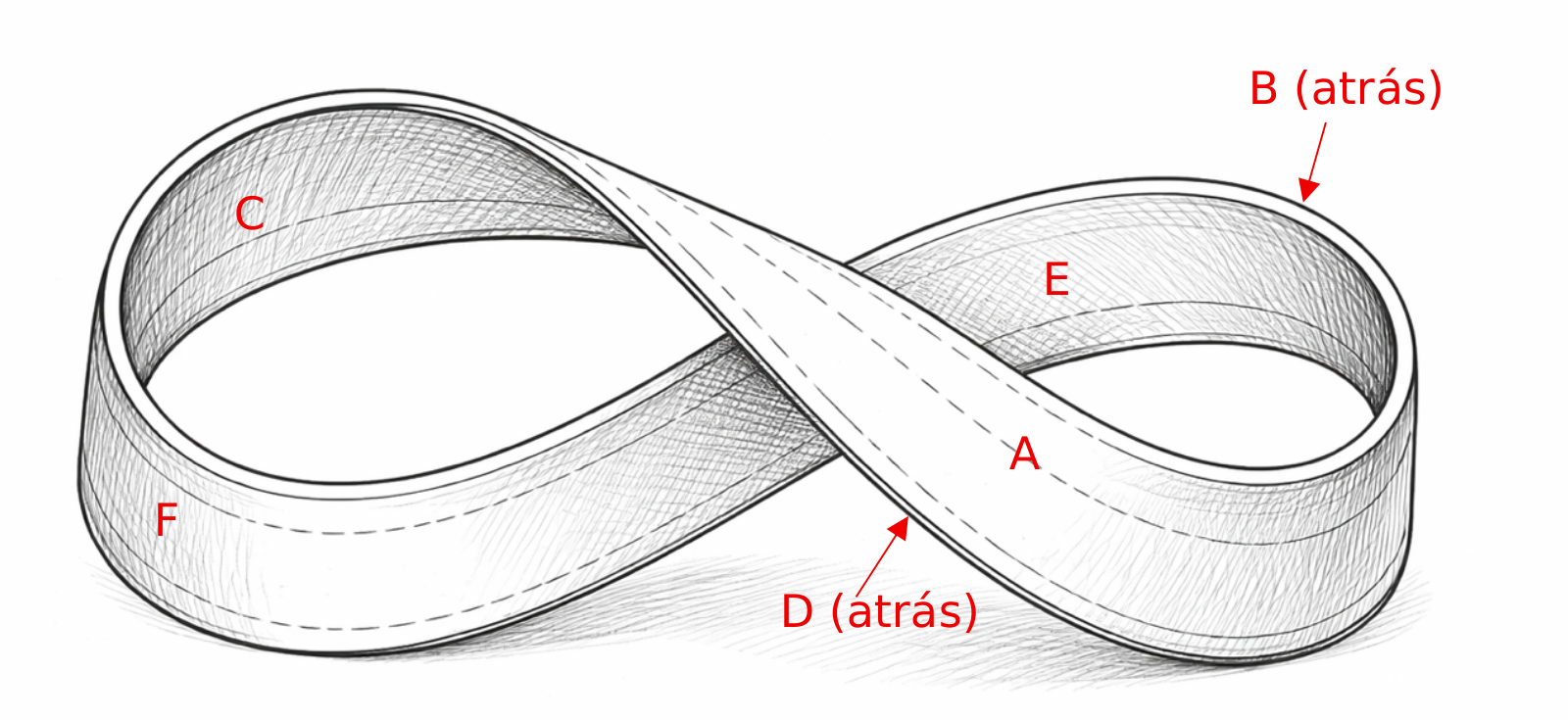
El lector puede seguir con la mirada (o con un lápiz) lo que sucedería si una hormiga comienza a caminar a lo largo de la banda, sin nunca invertir su dirección. Si comienza en el punto A, pasará por el punto B, después el C, el D, el E, el F y finalmente regresa a A. Le dio toda la vuelta a la banda que, como vemos, tiene un solo lado. Si la hormiga comenzara pintando de verde las regiones de la banda que atraviesa, coloraría toda la banda con un solo color. Eso quiere decir que la banda de Möbius tiene un solo lado. Igualmente fácil es comprobar que si la hormiga recorriera la orilla de la banda, regresaría al mismo lugar. Es decir, la superficie de la banda es de tamaño finito, pero está limitada por un solo margen.
La construcción de la cinta es tan simple que lo sorprendente es que se le haya descrito matemáticamente hasta el siglo XIX. Hoy sabemos que en la antigüedad ya se conocía la banda, como muestra la figura inferior, del dios de la eternidad, apoyándose en una banda de Möbius en la que se han pintado los signos del zodiaco.

Es fácil entender por qué el dios de la eternidad se podría interesar en la banda de Möbius, ya que esta se presta para representar el movimiento infinito del cosmos. También sabemos hoy que cadenas planas configuradas como la banda de Möbius fueron utilizadas por los ingenieros de la antigüedad para operar mecanismos con poleas, ya que de esa manera la cadena solo tiene un lado, y no dos, de manera que todas sus partes se desgastan por igual por la fricción con la polea.
La banda de Möbius es interesante para los matemáticos, porque en el campo de la llamada topología interesa entender las propiedades de superficies o sólidos, su orientabilidad, el número de lados que poseen, etc. La banda es el ejemplo más simple de una superficie en tres dimensiones con un solo lado.
Para aquellos interesados en los trucos mágicos, la banda de Möbius también depara una sorpresa: se puede cortar la banda con una navaja, siguiendo el centro, hasta regresar al punto de partida y el resultado no es la separación de la banda de Möbius en dos partes. Al final tenemos una sola banda, del doble de largo, y que ya no es de Möbius, porque tiene dos lados.
También los arquitectos se han interesado por la banda de Möbius. El edificio, en la ilustración, es un buen ejemplo de un techo y paredes construidos como una banda de Möbius.









